hashmap 时间复杂度 |

理解时间复杂度以及Hash

常用数据结构时间复杂度

数据结构	根据关键字查找	根据索引查找	插入	删除
数组	O(n)	O(1)	O(n)	O(n)
有序数组	O(logn)	O(1)	O(n)	O(n)
链表	O(n)	O(n)	O(1)	O(1)
有序链表	O(n)	O(n)	O(1)	O(1)
双向链表	O(n)	O(n)	O(1)	O(1)
二叉树（一般情况）	O(logn)		O(logn)	O(logn)
二叉树（最坏情况）	O(n)		O(n)	O(n)
平衡树	O(logn)	O(logn)	O(logn)	O(logn)
排序二叉树	O(logn)~O(n)	O(logn)~O(n)	O(logn)~O(n)	O(logn)~O(n)
哈希表	O(1)		O(1)	O(1)

hash

hash 是将数据离散的一种算法，根据 key 来获取 value，核心在与 hash 函数的实现：

index = f(key, array_size)

常用方法：

除留余数法 h(k) = k mod p
平方散列法 h(k) = k*k >> 28
斐波那契（Fibonacci）散列法 h(k) = (value * 2654435769) >> 28

hash collision resolution

hash 为了达成 O(1) 的时间复杂度，需要保证数据完全离散，当 hash 时根据选择的方法会产生碰撞，这是需要解决碰撞以保证离散散列

Separate chaining
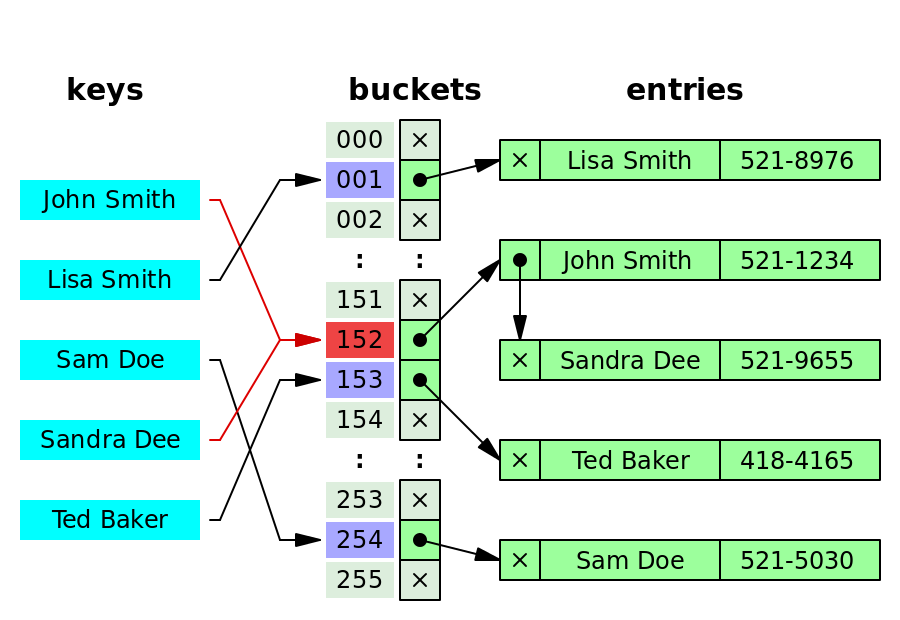
Open addressing

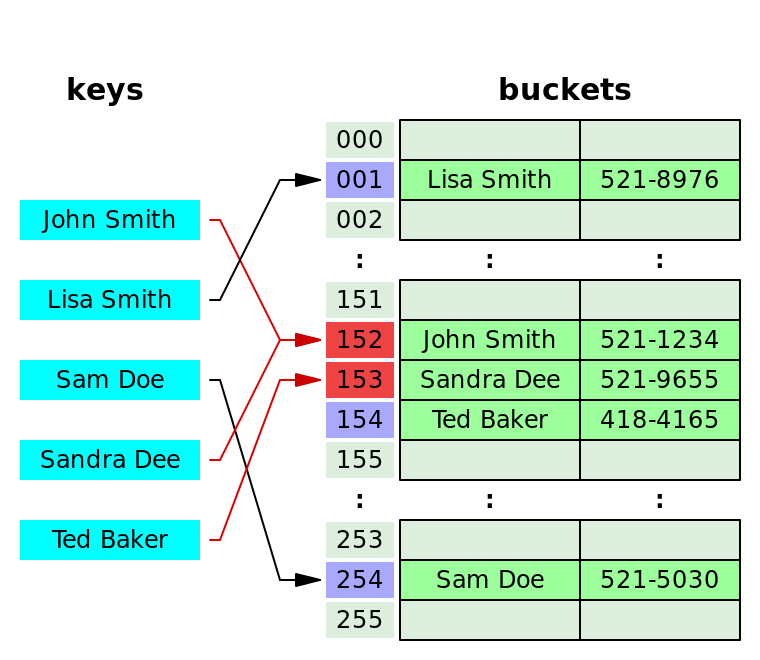
关于以上几种解决碰撞的优缺点比较见 Hashing | Set 3 (Open Addressing)

链表法计算简单，计算量少
链表法不会填满
链表易于删除插入
链表法对散列函数和装载因子不敏感，开地址法为避免聚类和性能下降

Open addressing requires extra care for to avoid clustering and load factor.
当数据量以及插入删除频率不确定时使用链表法，反之使用开地址法
链表法需要额外的存储空间
链表法可能浪费空间，部分hash项未使用
链表的缓存性能不佳

hash load factor

泊松分布选择 0.75

数据量固定时也可以选择开地址法构建 hashmap
当数据量固定时选择 4/3倍 以使数据离散减少碰撞
当数据量不固定时达到装载因子时进行扩容

separate chaining

#include <stdio.h>
#include <stdlib.h>

struct node {
    int key;
    int val;
    struct node *next;
};

struct table {
    int size;
    struct node **list;
};

struct table *createTable(int size)
{
    struct table *t = (struct table *)malloc(sizeof(struct table));
    t->size = size;
    t->list = (struct node **)malloc(sizeof(struct node *)*size);
    int i;
    for (i = 0; i < size; i++)
        t->list[i] = NULL;
    return t;
}

int hashCode(struct table *t, int key)
{
    if (key < 0)
        return -(key % t->size);
    return key % t->size;
}

void insert(struct table *t, int key, int val)
{
    int pos = hashCode(t, key);
    struct node *list = t->list[pos];
    struct node *newNode = (struct node *)malloc(sizeof(struct node));
    struct node *temp = list;
    while (temp) {
        if (temp->key == key) {
            temp->val = val;
            return;
        }
        temp = temp->next;
    }
    newNode->key = key;
    newNode->val = val;
    newNode->next = list;
    t->list[pos] = newNode;
}

int lookup(struct table *t, int key)
{
    printf("lookup key %d\n", key);
    int pos = hashCode(t, key);
    struct node *list = t->list[pos];
    struct node *temp = list;
    while (temp) {
        if (temp->key == key) {
            printf("(%d, %d)\n", temp->key, temp->val);
            return temp->val;
        }
        printf("(%d, %d) -> ", temp->key, temp->val);
        temp = temp->next;
    }
    return -1;
}

void display(struct table *t, int size)
{
    int i = 0;
    for (i = 0; i < size; i++) {
        printf("[%d]", i);
        struct node *temp = t->list[i];
        while(temp) {
            printf("(%d, %d)", temp->key, temp->val);
            temp = temp->next;
        }
        printf("\n");
    }
}

int main()
{
    struct table *t = createTable(10);
    insert(t, 2, 3);
    insert(t, 1, 20);
    insert(t, 22, 70);
    insert(t, 42, 80);
    insert(t, 4, 25);
    insert(t, 12, 44);
    insert(t, 14, 32);
    insert(t, 17, 11);
    insert(t, 13, 78);
    insert(t, 37, 97);
    display(t, 10);
    lookup(t, 2);
    return 0;
}

hashmap如下

$ ./a.out
[0]
[1](1, 20)
[2](12, 44)(42, 80)(22, 70)(2, 3)
[3](13, 78)
[4](14, 32)(4, 25)
[5]
[6]
[7](37, 97)(17, 11)
[8]
[9]
lookup key 2
(12, 44) -> (42, 80) -> (22, 70) -> (2, 3)

open addressing

#include <stdio.h>
#include <stdlib.h>

struct node {
    int key;
    int val;
};

struct table {
    int size;
    struct node **list;
};

struct table *createTable(int size)
{
    struct table *t = (struct table *)malloc(sizeof(struct table));
    t->size = size;
    t->list = (struct node **)malloc(sizeof(struct node *)*size);
    int i;
    for (i = 0; i < size; i++)
        t->list[i] = NULL;
    return t;
}

int hashCode(struct table *t, int key)
{
    if (key < 0)
        return -(key % t->size);
    return key % t->size;
}

void insert(struct table *t, int key, int val)
{
    int pos = hashCode(t, key);
    int n = 0;

    printf("\033[1;32mInsert (%d, %d) in %d\n\033[0m", key, val, pos);
    while(t->list[pos]) {
        printf("(%d, %d) -> ", t->list[pos]->key, t->list[pos]->val);
        pos = hashCode(t, pos + 1);
        n++;
        if (n == t->size)
            break;
    }

    if (n == t->size)
        printf("Hash table was full of elements\nNo Place to insert this element\n\n");
    else {
        struct node *newNode = (struct node *)malloc(sizeof(struct node));
        newNode->key = key;
        newNode->val = val;
        t->list[pos] = newNode;
        printf("(%d, %d)\n", key, val);
    }

    struct node *list = t->list[pos];
}

int lookup(struct table *t, int key)
{
    int pos = hashCode(t, key);
    int n = 0;

    printf("lookup key %d\n", key);
    while (n != t->size) {
        if (t->list[pos] && t->list[pos]->key == key) {
            printf("(%d, %d)\n", t->list[pos]->key, t->list[pos]->val);
            printf("Element found at index %d\n",pos);
            break;
        }
        else {
            if (t->list[pos])
                printf("(%d, %d) -> ", t->list[pos]->key, t->list[pos]->val);
            pos = hashCode(t, pos + 1);
        }
    }

    return -1;
}

void display(struct table *t, int size)
{
    int i = 0;
    for (i = 0; i < size; i++) {
        printf("[%d]", i);
        struct node *temp = t->list[i];
        printf("(%d, %d)", temp->key, temp->val);
        printf("\n");
    }
}

int main()
{
    struct table *t = createTable(10);
    insert(t, 2, 3);
    insert(t, 1, 20);
    insert(t, 22, 70);
    insert(t, 42, 80);
    insert(t, 4, 25);
    insert(t, 12, 44);
    insert(t, 14, 32);
    insert(t, 17, 11);
    insert(t, 13, 78);
    insert(t, 37, 97);
    display(t, 10);
    printf("%d\n", lookup(t, 13));
    return 0;
}